How to Use Partial Least Squares to Conduct Relative Importance Analysis

Introduction

There are a number of different approaches to calculating relative importance analysis, this article will briefly describe an alternative method - Partial Least Squares.

Partial Least Squares (PLS) is a popular method for relative importance analysis in fields where the data typically includes more predictors than observations. It is a dimension reduction technique with some similarity to principal component analysis. The predictor variables are mapped to a smaller set of variables and within that smaller space, we perform a regression against the outcome variable. In contrast to principal component analysis where the dimension reduction ignores the outcome variable, the PLS procedure aims to choose new mapped variables that maximally explain the outcome variable.

Requirements

1. Open a project in Q.
2. Load some data into the project. In this example, we are going to load the data using File > Data Sets > Add to Project > From URL and paste in this link: http://wiki.q-researchsoftware.com/images/6/69/Stacked_Cola_Brand_Associations.sav

Method

PLS is not available in the menus of Q, but we can get to it by typing a few lines of code.

1. From the Create menu select R Output 
2. Enter the following snippet of code:

   dat = data.frame(Q6_, Q5_0_, Q5_1_, Q5_2_, Q5_3_, Q5_4_, Q5_5_, Q5_6_, Q5_7_, Q5_8_, 
   Q5_9_, Q5_10_, Q5_11_, Q5_12_, Q5_13_, Q5_14_, Q5_15_, Q5_16_, Q5_17_,
   Q5_18_, Q5_19_, Q5_20_, Q5_21_, Q5_22_, Q5_23_, Q5_24_, Q5_25_, Q5_26_,
   Q5_27_, Q5_29_, Q5_28_, Q5_30_, Q5_31_, Q5_32_, Q5_33_)
   
   library(pls)
   library(flipFormat)
   library(flipTransformations)
   
   dat = AsNumeric(ProcessQVariables(dat), binary = FALSE, remove.first = FALSE)
   pls.model = plsr(Q6_ ~ ., data = dat, validation = "CV")

   
   The first line selects Q6_ as the outcome variable (strength of preference for a brand) and then adds 34 predictor variables, each indicating whether the respondent perceives the brand to have a particular characteristic. In your project, these variables can be dragged across from the Data Sets tree on the left into the R CODE window rather than typing them in one by one.
   
   Next, the 3 libraries containing useful functions are loaded. The package pls contains the function to estimate the PLS model, and Displayr's publicly available packages, flipFormat, and flipTransformations are included to help transform and tidy the data. Since the R pls package requires inputs to be numerical, I converted the variables from categorical.
   
   In the final line above the plsr function does the work and creates pls.model.
3. Adding the following lines recreates the model with the optimal number of dimensions:

   # Find the number of dimensions with lowest cross validation error
   cv = RMSEP(pls.model)
   best.dims = which.min(cv$val[estimate = "adjCV", , ]) - 1
   # Rerun the model
   pls.model = plsr(pref ~ ., data = dat, ncomp = best.dims)

   You will need to replace pref on the last line of code with your outcome variable. In this example, I used Q6_ as the outcome variable.
4. Finally, extract the useful information and format the output by adding the following lines of code:

   coefficients = coef(pls.model)
   sum.coef = sum(sapply(coefficients, abs))
   coefficients = coefficients * 100 / sum.coef
   names(coefficients) = TidyLabels(Labels(dat)[-1])
   coefficients = sort(coefficients, decreasing = TRUE)

   The regression coefficients are normalized so their absolute sum is 100. The labels are added and the result is sorted.
   
   The results below show Reliable and Fun are positive predictors of preference, Unconventional and Sleepy are negative predictors, and Tough has little relevance.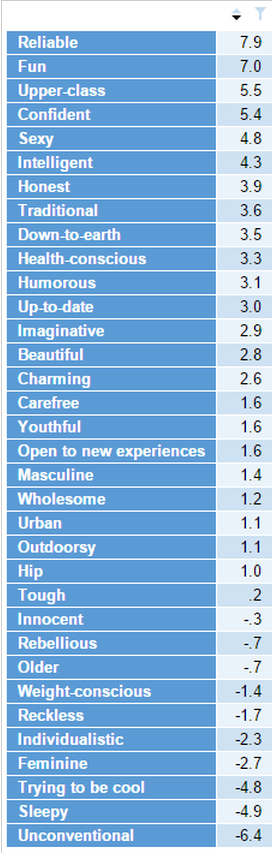
   
   

Next

How to Make an Importance/Performance Scatterplot in Q