How to Use Indifference Curves to Understand Trade-offs in Conjoint Analysis

Introduction

Indifference curves are a way of showing relative preferences for quantities of two things (e.g., preferences for price versus delivery times for fast food). This post shows how to compute indifference curves for conjoint analysis models.

Example

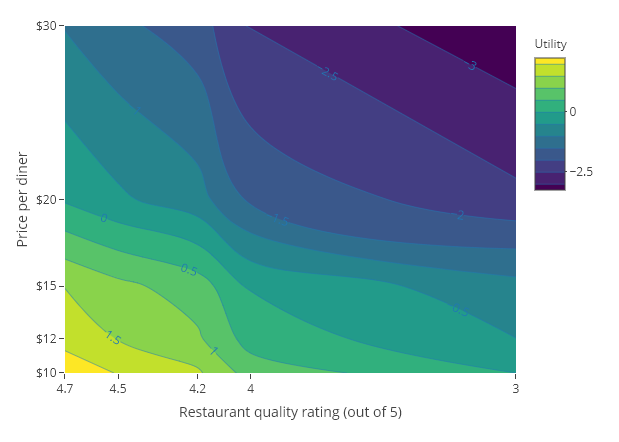
The contour plot below shows indifference between price and meal quality, from a choice-based conjoint study of home delivery preferences in the United States. It is read as follows:

People prefer low prices and high quality (i.e., the utilities are highest at the bottom-left and lowest at the top-right).
The bottom-right corner shows that the utility for a restaurant with a quality rating of 3.0 and a price of $10 per diner, has a utility of around about 0 (read from the legend).
If we follow the curve from the bottom-right corner up to where it is at a restaurant quality of 4, we can see that this equates to a price of around $15. This tells us that:
3/5 quality + $10 = 4/5 quality + $15. Putting it a different way, it tells us that improving quality from 3 to 4 out of 5 is worth about an average of $5 to the average diner.
Following the curve all the way to the left of the plot, we can see that:
3/5 quality + $10 = 4/5 quality + $15 = 4.7/5 quality + $20
The sweet spot is to have price less than $20 and quality more than 4. It’s impossible to have a high utility without both of these.

Requirements

A document containing a Latent Class Analysis, Hierarchical Bayes or Ensemble Choice Model output created in Q.

Method

The first step in computing indifference curves is to compute the average utilities for the attribute levels being evaluated. These are obtained by

Estimating a choice model in Q,
Selecting the model
Clicking Automate > Browse Online Library > Conjoint/Choice Modeling > Save Variable(s) > Individual-Level Coefficients.

Step 2: Create an indifference table

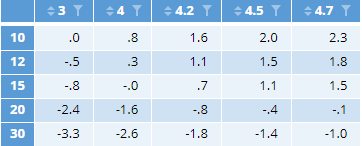
The utility of combinations of different attribute levels is computed by addition. For example, the utility of $30 price per person and an average rating of 4.7 (scroll down in the table), is -3.3 +2.3 = -1.0. The table below shows the calculations for all combinations of price and quality rating. Alternatively, you can create indifference curves for market or preference share using a simulator.

x = table.Individual.level.coefficients.from.choice.model.no.low.rlh
utilities.review = matrix(x[34:38], nrow = 5, ncol = 5, byrow = TRUE)
utilities.price = matrix(x[5:9], nrow = 5, ncol = 5, byrow = FALSE)
u = utilities.review + utilities.price
dimnames(u) = list("Price per diner" = c(10, 12, 15, 20, 30), "Restaurant quality rating (out of 5)" = c(3, 4, 4.2, 4.5, 4.7))
indifference.table = u

Step 3: Create the contour plot

The final stage is to create a contour plot (essentially a type of heatmap) where curves interpolate between all the points on the indifference table. The code below uses the plotly R package to create the indifference curve shown at the beginning of the post.

IndifferenceCurves <- function(X, x.tick.format = "", y.tick.format = "", x.reverse = FALSE, y.reverse = FALSE, show.hover = FALSE)
{
x.name = names(dimnames(X))[2]
y.name = names(dimnames(X))[1]
require(plotly)
hover = paste0(y.name, ": %s\n", x.name, ": %s\nUtility: %.2f") 
hover = sprintf(hover, rownames(X), rep(colnames(X), rep(nrow(X), ncol(X))), as.numeric((X)))
hover = matrix(hover, nrow = nrow(X), byrow = FALSE)
plot_ly(x = as.numeric(colnames(X)), 
y = as.numeric(rownames(X)), 
z = X, 
type = "contour" ,
text = if(show.hover) hover else NULL, 
hoverinfo = "text",
contours = list(showlabels = TRUE)) %>%
colorbar(title = "Utility") %>% 
config(displayModeBar = F) %>% 
layout(xaxis = list(title = x.name, 
tickformat = x.tick.format, 
tickvals = colnames(X),
autorange = if (x.reverse) 'reversed' else TRUE), 
yaxis = list(title = y.name,
tickformat = y.tick.format, 
tickvals = rownames(X),
autorange = if (y.reverse) 'reversed' else TRUE))
}
IndifferenceCurves(indifference.table, y.tick.format = "$", x.reverse = TRUE)

Articles in this section